Editorial Quick Take
Fractal geometry is not just a chapter of mathematics, but one that helps Everyman to see the same world differently.
Benoit Mandelbrot, The Fractal Geometry of Nature
Just how long is the Pacific coastline of the United States?
According to the U.S. state department the coastlines of Washington, Oregon and California together measure 2,131 km. This would seem to settle things. But the National Oceanic and Atmospheric Administration (N.O.A.A.) says that number should be 3,288 km. It seems at least one of these agencies must have measured … poorly.
However, this difference in the agencies’ reporting merely illustrates what mathematicians call the “coastline paradox.” In light of this paradox, neither agency is right and neither wrong. It would be equally valid to say that the Pacific coast was 2,131 km long or 3,288 km long … or even 17,462 km long. This has to do with the fractal dimension of coastlines. Like many objects in nature, coastlines have fractal dimension. Their apparent complexity remains the same even at a smaller and smaller scale.
To begin to understand fractal dimension and its impact upon measurement, imagine what it would take to measure the coast of Oregon. To find the approximate length, we could run a string (represented by the yellow line) as carefully as possible down the coastline, straighten it back out, and measure it.
That seems simple enough:
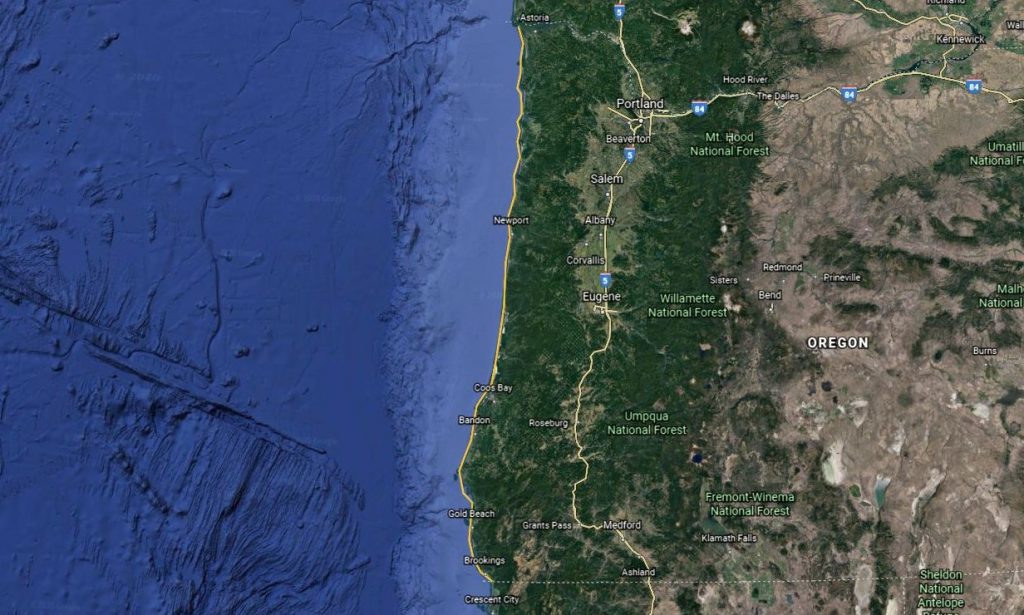
But it turns out that measuring a coastline is quite a bit more complicated.
Zoom in on the portion of the coast from the mouth of the Columbia River to Neskowin and you can see that there are numerous capes, inlets, and other features of the coastline that our previous measurement did not account for (the yellow line being the original estimate).
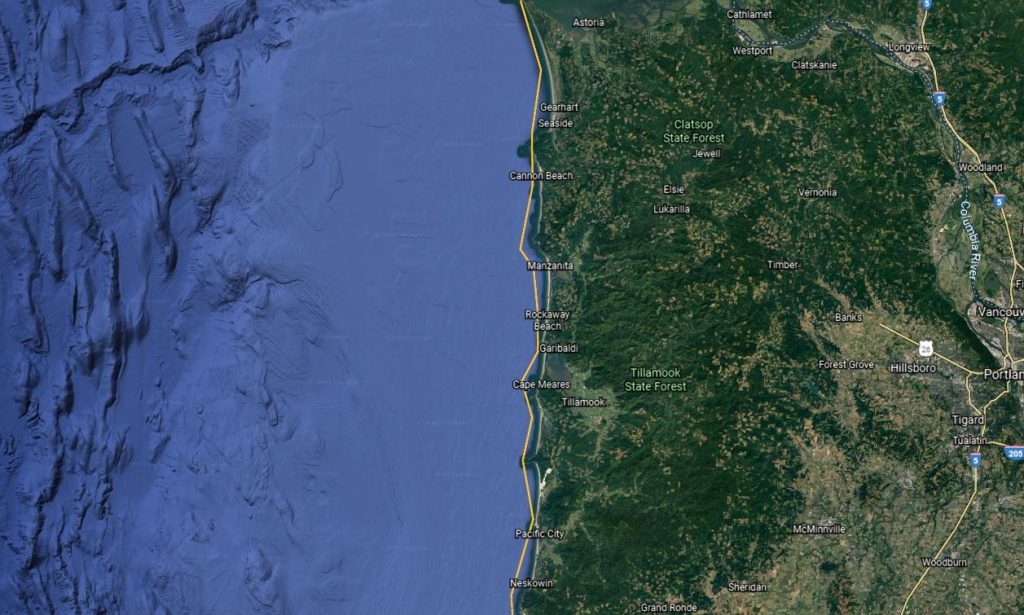
In order to get a more accurate measurement of the coastline, then, we need to ‘poke’ the string into all those little spaces, as below. Because of all of those extra curves and turns, the ‘string’ is going to end up longer if we match the contours more closely.
That is better, but look what happens to our so-called ‘more accurate’ measurement if we continue to look more closely. The slideshow below shows the effect of the magnification as we zoom in from the entire coast all the way to a rocky outcropping on the inland side of Wells Cove, a feature of Cape Lookout. It may not look like it, but each magnification lengthens the previous measurement by around 1.2 times, some more or some less based upon ‘roughness.’
(click the center to play the slideshow)
How much of an impact do these magnifications have on the overall length?
The comparison below shows the effect of such detail on the overall measurement of Arch Cape. The increased detail on the right nearly doubles the length of the cape’s coastline!

Though Google images lose resolution at some point, we could theoretically continue zooming in further and further until we would be mapping not only the traditional contours of the coast, but even the nooks and crannies on the surfaces of rocks! The greater the detail, the greater the length we will find.
So because coastal features have a fractal dimension the length of the Pacific coast can credibly be described as approaching infinity and essentially unmeasurable in the ordinary sense of that word.
Below is one last illustration showing the increasing length of the Pacific coast as the measurement takes into account greater and greater roughness, ending in a distance close to that established by the state department, but nowhere near the measurement we would get if we used the level of detail in the second take on Arch Cape above.
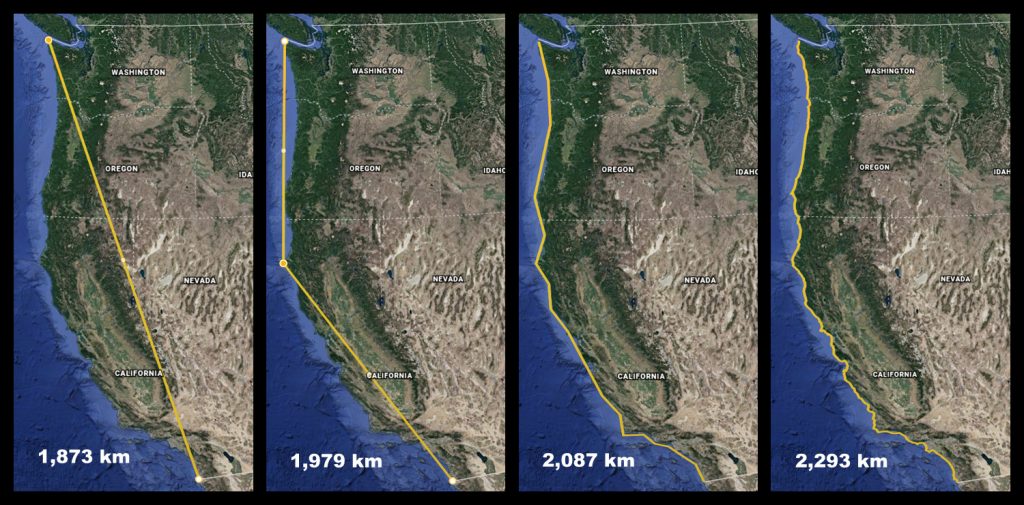
Before closing, it should be noted that when it comes to tidal shoreline, N.O.A.A. says the Pacific coast has 64,853 km of it; and the U.S. army measures it at 85,130 km. But that is for another day, another definition, and another debate between California and Maine that involves more than the electoral college.
Interested in playing around with coastline measurement? Explore Google Earth for yourself. (It’s free.) Find a coastline near you and try out their measurement function at different magnifications. (Click on the icon that looks like a ruler in the left toolbar.)
For more on fractals, following the links in the article, read Benoit Mandelbrot’s original essay, “How Long is the Coast of Britain? Statistical Self-Similarity and Fractal Dimension“ or watch his TED talk on “Fractals and the Art of Roughness” below.
Header Image: photo of the Oregon, Arcadia Beach State Recreation Area, Jon Balsbaugh
All map images from Google Earth.






3 Comments
Caleb Dahl
Splendid!
Pingback:
Pingback: