No matter how long ago you studied math in high school, you probably remember using a compass and a straightedge to do basic geometric constructions. Perhaps you were asked to use these tools to find the midpoint of a line segment, bisect an angle, or even construct a hexagon (Illustration A). With its overlap between mathematics and art, many students count geometry as among the best of their mathematical experiences.
You may also remember being told that it was impossible to trisect an angle using a compass and a straightedge. Maybe you were one of those students who just had to try it for yourself. If you did try, you didn’t suceed. Trisecting an angle is one of the three ‘impossible constructions’ (along with squaring the circle and doubling the cube.) While the ancients considered these problems simply obstinate and as-of-yet unsolved, in 1837 the young French mathematician Pierre Wantzel finally proved that it was indeed impossible. He published his findings in a little-noted article for Journal de Mathematique.
Like many brilliant young mathematicians, Wantzel was an interesting character. Sadly, he died at the age of 34, only a decade after the publication, and his proof was ignored for almost fifty years. Of Wantzel’s inability to achieve even greater results in mathematics, fellow mathematician Jean Claude Saint-Venant wrote:
“I believe that this is mostly due to the irregular manner in which he worked, to the excessive number of occupations in which he was engaged, to the continual movement and feverishness of his thoughts, and even to the abuse of his own facilities. Wantzel improvised more than he elaborated, he probably did not give himself the leisure nor the calm necessary to linger long on the same subject … Ordinarily, he worked evenings, not lying down until late; then he read, and took only a few hours of troubled sleep, making alternately wrong use of coffee and opium, and taking his meals at irregular hours until he was married. He put unlimited trust in his constitution, very strong by nature, which he taunted at pleasure by all sorts of abuse. He brought sadness to those who mourn his premature death.”
Nonetheless, Wantzel’s proof was eventually discovered, improved upon slightly, and widely accepted.
So it really is impossible to trisect an angle with a compass and straightedge. Your teachers were right. But it is not impossible to trisect an angle with simple manual tools.
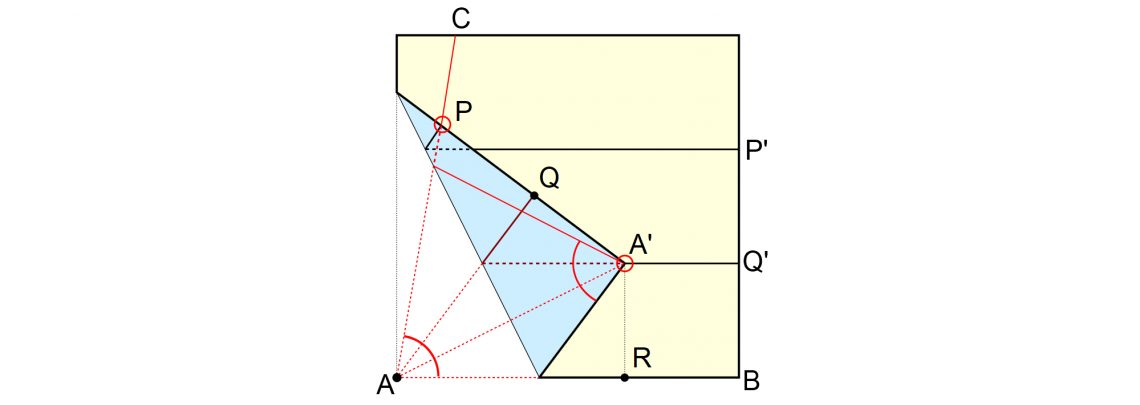
One solution comes to us from a surprising source, the ancient Japanese art of paper folding, origami. With only seven simple folds you can use a single piece of paper to trisect any arbitrary angle, something that is impossible with the classical compass and straightedge.
To try it yourself, follow along with the video below:
Origami constructions have been studied by
But if you think this means the Japanese were on to a kind of mathematics that the Greeks could never have had access to with their straightedges and compasses, there is a bit more to the story. (The video above may even be a bit misleading concerning the Greeks.)
While it is impossible to trisect an angle with a compass and a straightedge given the ordinary rules of those instruments, it is relatively easy to do so if one is willing to simply mark the straightedge with two dots.
The method is known as “neusis construction.” And despite the fact that the method had been shunned as inferior by Euclid in his Elements as well as by other classical mathematicians, no less an ancient thinker than Archimedes (287 – 212 B.C.) proved that it was possible to trisect an angle using this method.
So why would an effective method such as neusis construction ever be shunned?
To the Greeks’ sensibilities at the time, the more abstract and distant from physical reality a thing was, the nobler and more highly regarded. A method that required crudely marking off a segment of the theoretically infinite straight edge or the mathematically perfect circle in order to accomplish the task of trisection was considered somewhat vulgar.
As with the history of painting, the history of mathematics tells us that ‘approved’ technique is oftentimes as much a matter of philosophical commitments and aesthetic sensibilities as it is a matter of pure utility.
Perhaps it is a permanent feature of the human condition to believe that some things are just not worth doing unless they are worth doing beautifully and for the right reason.





6 Comments
Becca (Feeks) Brophy
Fascinating!
Matt Axvig
Aesthetics vs. Utility…is this why computer-assisted proofs are controversial?
Jon Balsbaugh
It seems to me that the controversy over computer-assisted proofs has a several-fold origin, perhaps rooted in the same objection:
1. Computer-assisted proofs take the human being out of the driver seat in being able to ‘peer review’ every aspect of the proof. They can’t be checked by hand. (Connect to driverless cars … even if they are statistically safer, people fear the loss of the human element to override the machine.)
2. There is a sense of unfair ‘advantage’ in what can be a highly competitive arena. (Connect to steroids in cycling and elsewhere in sports.)
3. And, yes, it is an ‘ugly’ way to do math even if it works.
I wonder what is most fundamental?
Abbey von Gohren
Gives a whole new perspective on what we mean when we say something is “impossible.”
Akangka
I thought Greeks trisect an angle by conic sections.
fernando mancebo
Angle trisection